Division Strategies for Grade 4 and Grade 5

This article discusses four division strategies. Additionally, you will find solved examples with explanations and links to worksheets for extra practice or assessment.

What is Division?

One of the four basic math operations, along with addition, subtraction, and multiplication, is division.

Division is the process of splitting a larger group into smaller groups so that each group contains an equal number of items.

Mathematicians use this operation to group and distribute resources equally.

Division is the inverse of multiplication. When dividing numbers, we break down a larger number into smaller ones such that the multiplication of the smaller numbers will be equal to the larger number.

For example, 10 ÷ 2 = 5. We can express this as the multiplication fact 2 x 5 = 10.

Join my email list and download freebies from my Free Resource Library.

Please leave this field empty

First name *

Email address *

Success! Please check your email to confirm for the password and link to Freebie library.

Division Symbols

We can represent the division of two numbers by one of two fundamental division symbols (÷ and /). 

For example, 10 ÷ 2 = 5, and 10/2 = 5.

The mathematical symbol that looks like a small horizontal line with dots above and below it is the one mostly used to represent division.

Parts of Division

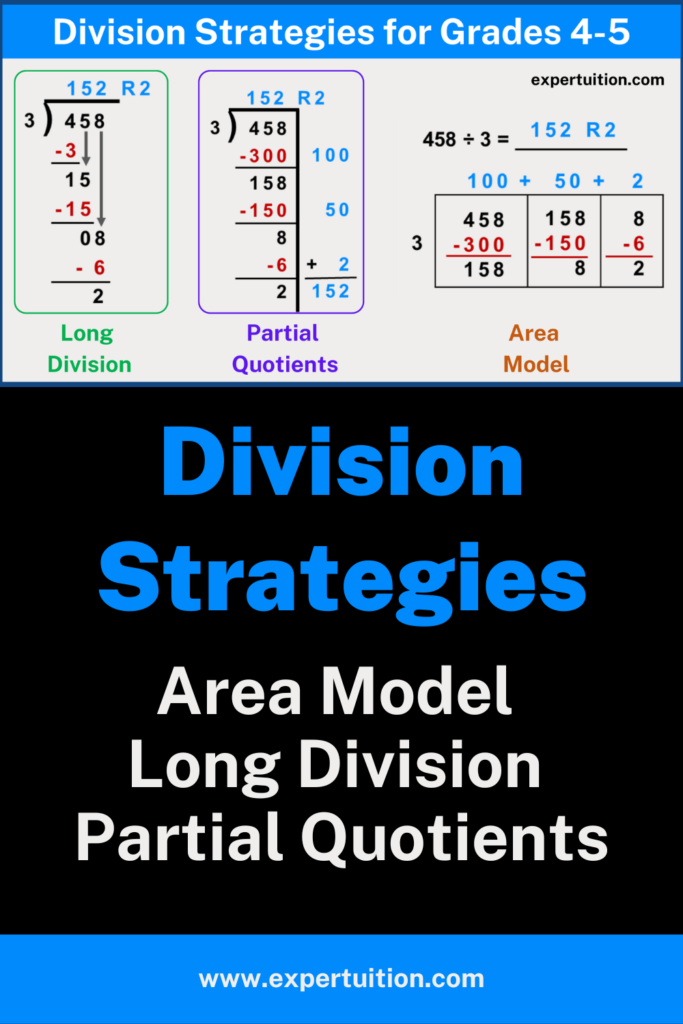
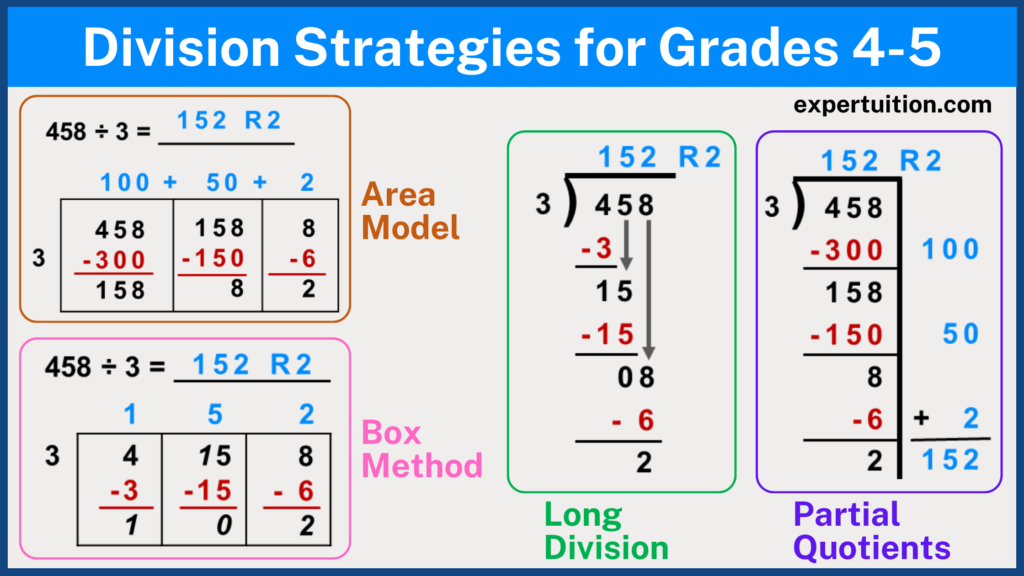
A division problem is made up of the following four components: dividend, divisor, quotient, and remainder. In the division equation 458 ÷ 3 = 152 R2;

• the dividend (458) is the number that is to be divided (the first number on the left)
• the divisor (3) is the number by which we divide the dividend (the second number after the division symbol)
• the quotient (152) is the answer obtained after performing the division (number on the right after the equal to symbol)
• the remainder (2) is the remaining value that is smaller than the divisor (the number attached to the quotient)

Division Strategies

We can use multiplication tables to divide small numbers.

For instance, to solve 10 ÷ 2, we only need to determine what we must multiply by 2 to obtain 10 as the answer.

Clearly, 2 × 5 = 10, therefore 10 ÷ 2 = 5.

However, it becomes nearly impossible to use this approach when dividing larger numbers.

We must therefore come up with alternate strategies to use when dividing larger numbers.

Some of such division strategies include;

1. Long Division
2. Partial Quotient Division
3. Area Model Division
4. Box Method Division

Using Long Division as a Division Strategy.

Long division is a method of dividing large numbers that breaks the problem down into multiple steps that are performed in a specific order.

We will be able to divide numbers of any length once we have mastered the steps of long division.

How to Divide Using the Long Division Method?

Following the steps outlined here, you can easily divide using long division.

1. Divide
2. Multiply
3. Subtract
4. Bring Down
5. Repeat the Process

To better understand long division, let’s try it with the example 458 ÷ 3.

Step 1 – Divide

Set up the equation. 

• Draw the long division symbol ⟌
• Write the divisor (3) on the left outside the symbol and dividend (458) on the right, under the division symbol.

Divide the first digit. 

• Working from left to right, determine how many times the divisor can go into the first digit of the dividend without exceeding it.
• In our example, you would want to know how many times 3 goes into 4, which is 1.
• If the divisor is a larger number than the first digit (138 ÷ 3), determine how many times the divisor goes into the first two digits of the dividend without exceeding it.
• In this case, you would want to know how many times 3 goes into 13, which is 4.

Enter the first digit of the quotient. 

• Place the number of times the divisor goes into the first digit (or first two digits) of the dividend on top of the division symbol above the appropriate digit.
• Long division requires that the number columns remain correctly aligned.
• In 458 ÷ 3, you would place a 1 above the 4, since we’re looking at how many times 3 goes into 4.
• In 138÷ 3, you would place a 4 above the 3, since we’re looking at how many times 3 goes into 13.

Join my email list and download freebies from my Free Resource Library.

Please leave this field empty

First name *

Email address *

Success! Please check your email to confirm for the password and link to Freebie library.

Step 2 – Multiply

Multiply and record the product. 

• Multiply the divisor by the digit of the quotient you just wrote above the dividend. (3 x 1 = 3 and 3 x 4 = 12).
• Write the result of your multiplication beneath the dividend.
• In the first example, write 3 beneath the 4 and 12 beneath the 13 in the second example, being careful to keep the numbers aligned.

Step 3 – Subtract

Subtract the product. 

• Draw a line beneath the product of the multiplication.
• Subtract the number (product of the multiplication) from the digits of the dividend directly above it.
• Write the result beneath the line you just drew.
• In the examples, subtract 3 from 4 to get 1 and 12 from 13 to get 1.

Step 4 – Bring Down

Bring down the next digit. 

• Because the divisor cannot go into the result of the subtraction operation, you need to bring down the next digit of the dividend (if present).
• In the first example, because 3 cannot go into 1 without exceeding it, you need to bring down the 5 from 458 and place it after the 1, making it 15, which 3 can go into.

Step 5 – Repeat the Process

Repeat the whole process. 

• Divide the new number by the divisor, and write the result above the dividend as the next digit of the quotient.
• In the example, determine how many times 3 can go into 15. Write that number (5) as the next digit of the quotient above the dividend.
• Then multiply 3 by 5, and subtract the result (15) from 15.
• If the dividend has more digits, keep repeating this process until you have worked through all of them (until you get zero or a number less than the divisor).

Record the remainder. 

• Record if there is a remainder, i.e., an indication of how much is left over after you have completed your division.
• In the example, the remainder would be 2, because 3 cannot go into 2, and there are no more digits to bring down.
• Place the remainder after the quotient with the letter “R” before it. In the example, the answer would be expressed as “152 R2.”

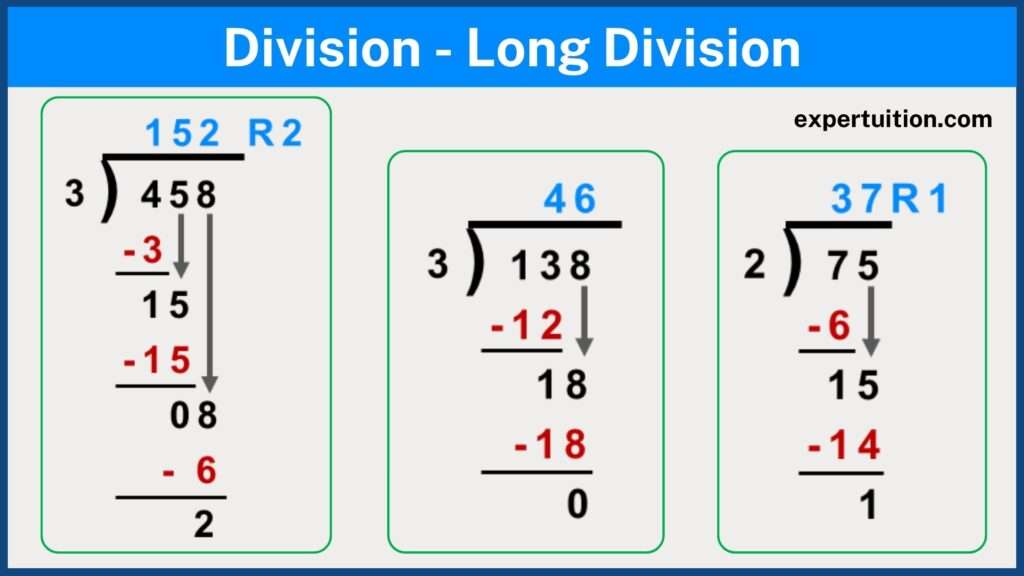
The same steps can be followed for division involving two-digit divisors.

Here, you find how many times the two-digit divisor goes into the first two or three digits of the dividend.

This is just like finding how many times a one-digit divisor goes into the first one or two digits of the dividend as discussed in the above steps.

Long Division Practice Worksheets and Task Cards

If you’re looking for engaging long division resources to use with your students, then my differentiated long division products will be the perfect fit for you.

You can get these division products from my TPT store or my WooCommerce shop.

Using Partial Quotients as a Division Strategy.

Division with partial quotients deviates from the standard method.

The partial quotients method encourages students to break division questions down into “friendlier” chunks.

To solve basic division problems, the partial quotients approach makes use of repeated subtraction.

How to Divide Using the Partial Quotients Method?

Following the steps outlined here, you can easily divide using the partial quotients method.

1. Find and subtract an easy multiple
2. Repeat the process
3. Add the partial quotients

To better understand partial quotients division, let’s try it with the example 458 ÷ 3.

Step 1 – Find and subtract an easy multiple

Set up the problem (458 ÷ 3)

• Set up the problem like a long division equation.
• Draw a vertical line on the right.

Find an easy multiple of the divisor and subtract it from the dividend.

• To do this, multiply the divisor by a friendlier number such as 100, 10, 5, 2, etc. to get the easy multiple of the divisor. In the example, 3 x 100 = 300.
• The multiple of the divisor should be as close as possible to the dividend (less than or equal to the dividend).
• The factor or the number with which the divisor is multiplied is the partial quotient.
• Write the product or multiple (300) beneath the dividend (458) and the partial quotient (100) on the right side.
• Draw a line and subtract the multiple from the dividend (458 – 300 = 158)

Join my email list and download freebies from my Free Resource Library.

Please leave this field empty

First name *

Email address *

Success! Please check your email to confirm for the password and link to Freebie library.

Step 2 – Repeat the Process

Find another multiple of the divisor.

• Subtract the multiple from the difference (158) and write the partial quotient.
• Keep multiplying and subtracting until the difference is less than the divisor or equal to 0.
• If the difference is less than the divisor then that difference is the remainder.

Step 3 – Add the Partial Quotients

Add up the partial quotients to find the final quotient.

• Add up the partial quotients on the right.
• If there is a remainder, attach it to the final quotient to get your division answer. In the example, 458 ÷ 3 = 152 R2

The same steps can be used to divide by two digits. Find and subtract a multiple of the two-digit divisor from the dividend in the same way that you did with the one-digit divisor.

Long division lacks the flexibility of partial quotients division.

The long division must be done precisely, but with partial quotients, it is possible to simply subtract a multiple of the divisor from the dividend repeatedly and still get the correct answer.

You can use the partial quotients method to reinforce place value and the concept of division as repeated subtraction.

Partial Quotients Division Practice Worksheets

If you’re looking for engaging partial quotients division resources to use with your students, then my differentiated partial quotients division products will be the perfect fit for you.

You can get these division products from my TPT store or my WooCommerce shop.

Using Area Model as a Division Strategy.

The area model is an excellent way for visual learners to understand and conceptualize division while also improving their number sense.

The area model method, like the partial quotients method, employs repeated subtraction.

Also, an area model is a way of expressing division using rectangles.

The length and width of the rectangle are determined by the partial quotients and the divisor.

As a result, the rectangle will have the same number of columns as the number of partial quotients.

How to Divide Using the Area Model Method?

The area model method is similar to the partial quotients method in its steps, with the only difference being how the problem is presented.

1. Find and subtract an easy multiple
2. Repeat the process
3. Add the Partial Quotients

To better understand the area model division, let’s try it with the example 458 ÷ 3.

Step 1 – Find and subtract an easy multiple

Set up the problem (458 ÷ 3).

• Draw a rectangle and divide it into 2, 3, … columns (which will be as many as the number of partial quotients).
• Write the divisor (3) on the left outside the rectangle and the dividend (458) inside the first column leaving enough space below the number.

Find an easy multiple of the divisor and subtract it from the dividend.

• To do this, multiply the divisor by a friendlier number such as 100, 10, 5, 2, etc. to get the easy multiple of the divisor. In the example, 3 x 100 = 300.
• The multiple of the divisor should be as close as possible to the dividend (less than or equal to the dividend).
• The factor or the number with which the divisor is multiplied is the partial quotient.
• Write the partial quotient (100) on top of the first column and the multiple (300) beneath the dividend (458) inside the column.
• Draw a line and subtract the multiple from the dividend (458 – 300 = 158)

Join my email list and download freebies from my Free Resource Library.

Please leave this field empty

First name *

Email address *

Success! Please check your email to confirm for the password and link to Freebie library.

Step 2 – Repeat the Process

Write the difference between the dividend and the multiple (158) in the second column.

• Find another multiple of the divisor, subtract from the difference and write the partial quotient on top of the second column.
• Keep multiplying and subtracting until the difference is less than the divisor or equal to 0.
• If the difference is less than the divisor then that difference is the remainder.

Step 3 – Add the Partial Quotients

Add up the partial quotients to find the final quotient.

• Add up the numbers on top of the columns (partial quotients) to find your final quotient.
• If there is a remainder, attach it to the final quotient to get your division answer. In the example, 458 ÷ 3 = 152 R2

The same steps can be used to divide by two digits. Find and subtract a multiple of the two-digit divisor from the dividend in the same way that you did with the one-digit divisor.

Area Model Division Practice Worksheets

If you’re looking for engaging area model division resources to use with your students, then my differentiated area model division products will be the perfect fit for you.

You can get these division products from my TPT store or my WooCommerce shop.

Using Box Method as a Division Strategy.

Some educators call the box method the non-traditional long division method.

This is because the box method division strategy follows similar steps of breaking down a division problem like the traditional long division method.

Other educators refer to the box method as the area model division method.

This is because the box method division strategy follows the same visual representation as the area model, which uses rectangles to express division.

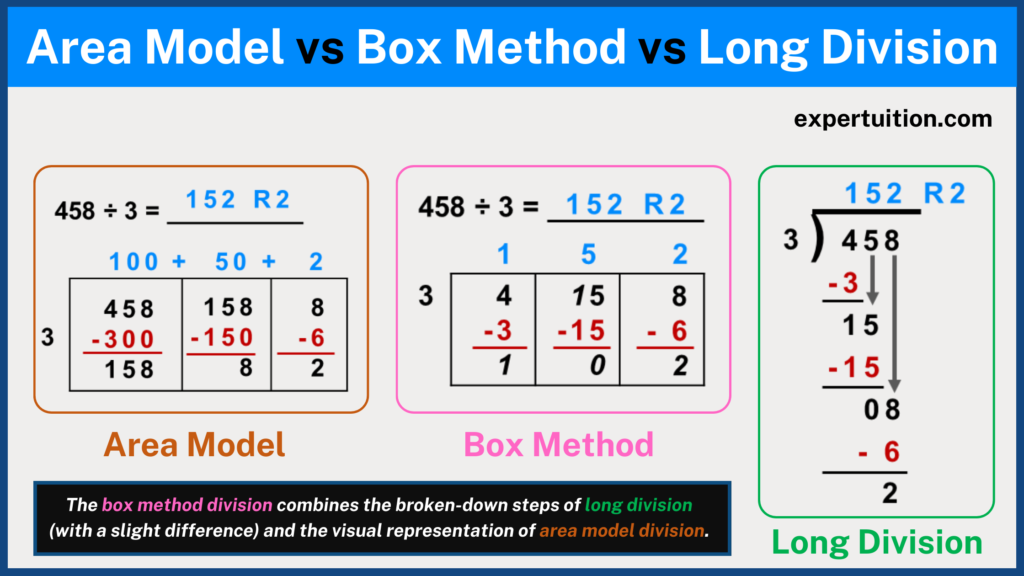
The box method division is the fusion of the area model and the long division methods.

It combines the broken-down steps of long division and the visual representation of area model division.

Many educators believe that the box method division is the easiest strategy for students to master division.

How to Divide Using the Box Method?

The box method is similar to the long division in its steps with only a slight difference. The 4th step is to Bring Up (instead of Bring down in long division).

1. Divide
2. Multiply
3. Subtract
4. Bring Up
5. Repeat the Process

To better understand box method division, let’s try it with the example 458 ÷ 3.

Step 1 – Divide

Set up the problem (458 ÷ 3).

• Draw a rectangle and divide it into 2, 3, or more columns depending on the number of digits in the dividend (the example will have 3 columns).
• Write the divisor (3) on the left outside the rectangle and the dividend (458) inside with a digit in each column, leaving enough space below the digits.

Divide the first digit. 

• Working from left to right, determine how many times the divisor can go into the first digit of the dividend without exceeding it.
• In our example, you would want to know how many times 3 goes into 4, which is 1.
• If the divisor is a larger number than the first digit, then the number of times the divisor can go into the first digit is zero.
• In 138 ÷ 3, you would want to know how many times 3 goes into 1, which is 0.

Enter the first digit of the quotient. 

• Place the number of times the divisor goes into the first digit of the dividend on top of the first column.
• In 458 ÷ 3, you would place a 1 on top of the first column above the 4.
• In 138÷ 3, you would place a 0 on top of the first column above the 1.

Join my email list and download freebies from my Free Resource Library.

Please leave this field empty

First name *

Email address *

Success! Please check your email to confirm for the password and link to Freebie library.

Step 2 – Multiply

Multiply and record the product. 

• Multiply the divisor by the digit of the quotient you just wrote on top of the column (3 x 1 = 3 and 3 x 0 = 0).
• Write the result of your multiplication beneath the digit in the first column.

Step 3 – Subtract

Subtract the product. 

• Draw a line beneath the product of the multiplication.
• Subtract the product from the digit of the dividend directly above it.
• Write the result beneath the line you just drew.
• In the examples, subtract 3 from 4 to get 1 and 0 from 1 to get 1.

Step 4 – Bring Up

Bring up the remainder. 

• Bring up the remainder to the next column and place it in front of the digit in the column.
• In the example (458 ÷ 3), bring up the remainder of 1 in the first column and place it in front of 5 in the second column making it 15.
• If there was no remainder in the first column, you can place 0 in front of the digit in the second column or leave it since it will not affect the division of the number in the second column.

Step 5 – Repeat the Process

Repeat the whole process. 

• Divide the number in the second column by the divisor, and write the result on top of the column as the next digit of the quotient.
• In the example, determine how many times 3 can go into 15. Write that number (5) as the next digit of the quotient on top of the column.
• Then multiply 3 by 5, and subtract the result (15) from 15.
• If the dividend has more digits left, keep repeating this process until you have worked through all of them.

Record the remainder. 

• Record if there is a remainder in the last column, i.e., an indication of how much is left over after you have completed your division.
• In the example, the remainder would be 2, since there are no more digits (columns) to bring up the remainder to.
• Place the remainder after the quotient with the letter “R” before it. In the example, the answer would be expressed as “152 R2.”

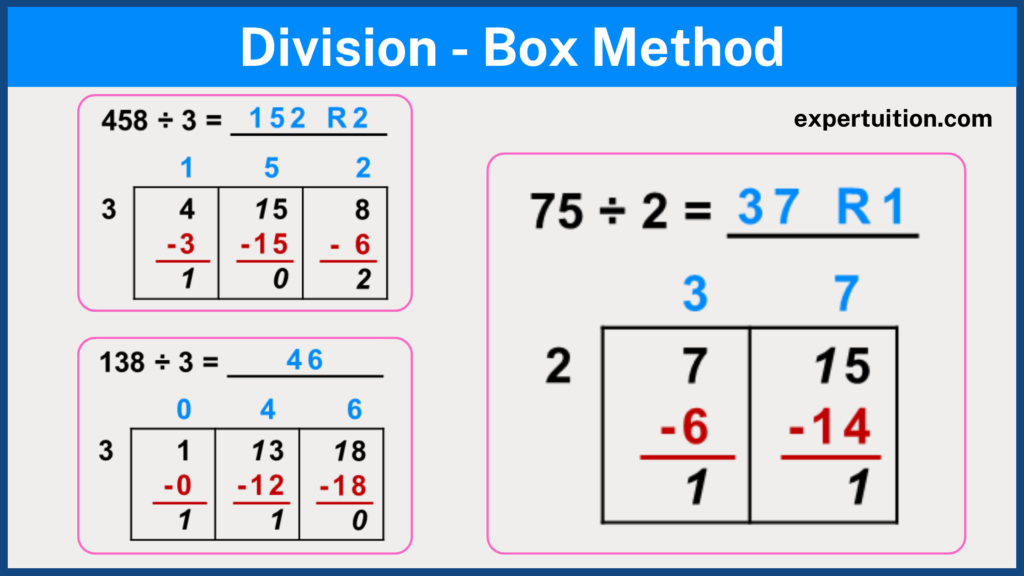
The same steps can be followed for division involving two-digit divisors.

Here, you find how many times the two-digit divisor goes into the first digit of the dividend in the first column which is zero.

Bring up the remainder from the first column to the second column and repeat the division steps as discussed above.

Box Method Division Practice Worksheets

If you’re looking for engaging box method division resources to use with your students, then my differentiated box method division products will be the perfect fit for you.

You can get these division products from my TPT store or my WooCommerce shop.

How do we verify our answer to a division problem?

In any division fact, the dividend is always equal to the product of the divisor and the quotient added to the remainder.

Thus, Dividend = (Divisor × Quotient) + Remainder.

The above formula helps us to verify the values of the quotient and the remainder obtained after performing division.

We can substitute the values of the quotient, remainder, and divisor in the equation to check if the result is the same as the dividend.

If the result is the same, we have correctly completed the division steps. If not, there is a problem with our calculations that needs to be fixed.

Let us verify the answer to our division problem: 458 ÷ 3 = 152 R2

Dividend = (Divisor × Quotient) + Remainder

458 = (3 × 152) + 2

458 = 456 + 2

thus, 458 = 458

The result is the same hence, it is verified that we have correctly answered the division problem.

Conclusion

Like other math operations, division is a life skill that kids or students need to master at an early age to help address some real-life problems.

In this article, four division strategies for multi-digit numbers were explained: long division, partial quotients division, area model division, and box method division.

Please leave this field empty

DOWNLOAD FREEBIES

Please, enter your NON-WORK EMAIL to ensure that you get the freebies!

First name *

Email Address *

We don’t spam! Read our privacy policy for more info.

Check your inbox or spam folder to confirm your subscription for the link to freebie library.