Multiplication Strategies for Grade 4 and Grade 5

This article discusses three multiplication strategies. Additionally, you will find solved examples with explanations and links to worksheets for extra practice or assessment.

What is multiplication?

Multiplication is one of the four basic arithmetic operations, along with addition, subtraction, and division.

The process of multiplication is the repeated addition of equal groups, which adds one number to itself multiple times.

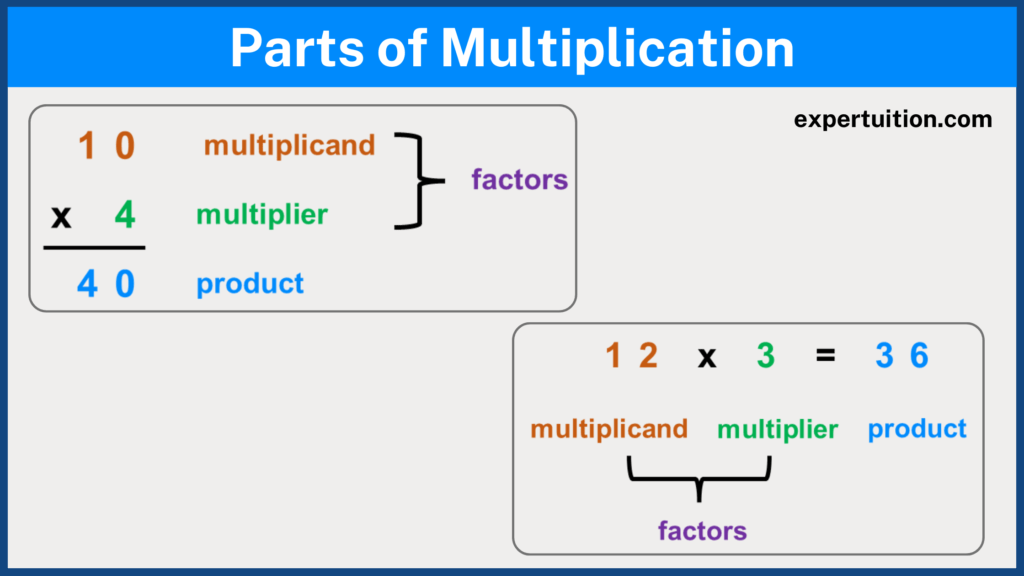
Parts of Multiplication

In the multiplication equation 10 x 4 = 40, the first number (10) is called the multiplicand and the second number (4) is called the multiplier.

The multiplicand and multiplier are known as factors and the answer (40) is known as the product.

Types of Multiplication

There are a variety of methods for multiplication available.

Teachers may require students to practice and employ particular methods in class, but each student must find the method that suits them the most.

Although we can use all multiplication methods to solve any multiplication problem, some methods are more suitable for a particular type of problem.

Repeated Addition Method

We usually use repeated addition to solve multiplication problems in grades below 4th and 5th. This multiplication method simply adds the same number repeatedly to itself.

For example, we can solve 10 x 4 by adding 10 to itself 4 times. Thus, 10 + 10 + 10 + 10 = 40.

This is a good strategy for small numbers or just a few groups of large numbers. Mentally, it is relatively easy to add multiples of ten and thus this method also works well.

Using this approach to multiply big numbers becomes tedious and error-prone.

For example, if you want to solve 83 x 64, you will have to add 83 to itself 64 times. This would take a lot of time and there is a high chance of making a mistake.

Join my email list and download freebies from my Free Resource Library.

Please leave this field empty

First name *

Email address *

Success! Please check your email to confirm for the password and link to Freebie library.

How do we multiply large numbers?

In fourth and fifth grades, some of the strategies for multiplying multi-digit large numbers include: 

1. partial product
2. area model
3. long multiplication

Partial Products Multiplication Strategy

The partial product method is applied to multiply numbers larger than 10. This method allows students to use the concept of place values to multiply numbers.

What is a Partial Product?

A partial product is a product obtained when we multiply a multi-digit multiplicand by one digit of a multi-digit multiplier. 

Partial products are a perfect way to learn the multiplication of multi-digit numbers.

This is a good multiplication strategy for improving number sense.

Steps for Partial Products Multiplication

In this method, we

1. set up the problem vertically
2. break the numbers into parts based on place value
3. find the products of the parts separately
4. add the separate products to find the final product

Partial Product Multiplication Examples

The following examples will help understand the concept of partial product multiplication. 

Partial product multiplication with a one-digit multiplier (54 x 2):

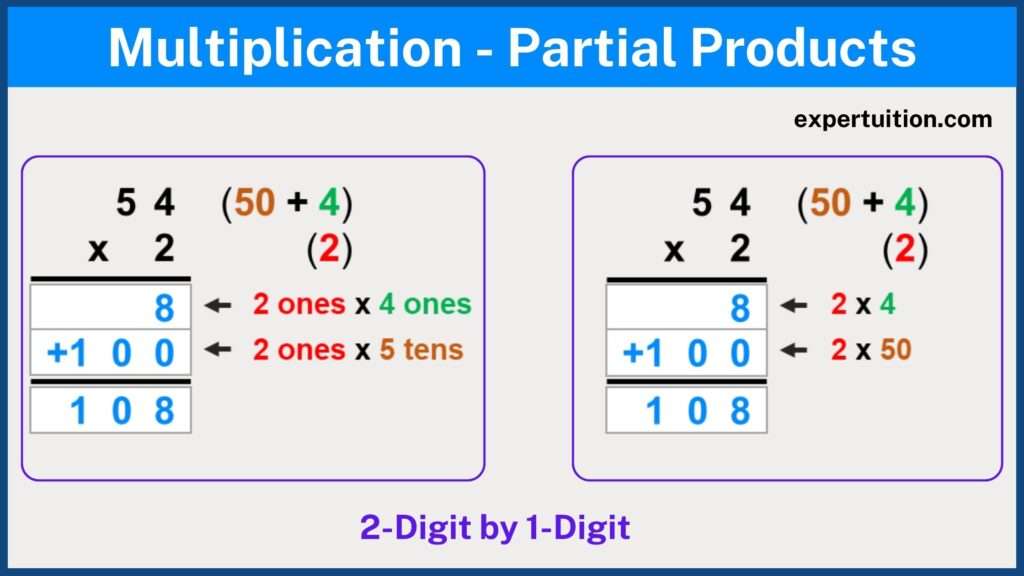
To multiply a 2-digit number by a 1-digit number using the partial product, follow the given steps: 

1. Write the numbers vertically, one above the other. The multiplicand should go on top.
2. Draw a horizontal line under the equation.
3. Break each number into parts based on its place value. Therefore, 54 = 50 + 4 and 2 = 2
4. Multiply the ones digit of the multiplier by the ones digit of the multiplicand and write down the product (2 x 4 = 8)
5. Next, multiply the ones digit of the multiplier by the tens digit of the multiplicand and write the product below the first product (2 x 50 = 100). 
6. Lastly, add up the two partial products to obtain the final answer (8 + 100 = 108).

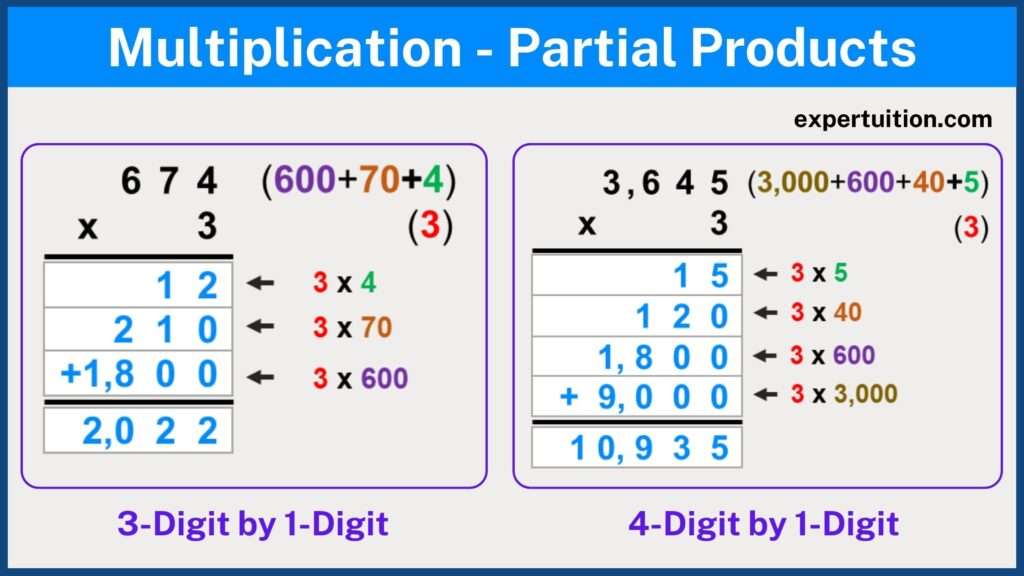
If the multiplicand has more than 2 digits, multiply the ones digit of the multiplier by the remaining digits of the multiplicand in the order (hundreds, thousands, etc.) before adding the partial products.

Partial product multiplication with a two-digit multiplier (65 x 23):

To multiply two 2-digit numbers using the partial product, follow the given steps: 

1. Write the numbers vertically, one above the other.
2. Draw a horizontal line under the equation.
3. Break each number into parts based on its place value. Therefore, 65 = 60 + 5 and 23 = 20 + 3
4. Multiply the ones digit of the multiplier by the ones digit of the multiplicand and write down the product (3 x 5 = 15).
5. Next, multiply the ones digit of the multiplier by the tens digit of the multiplicand and write down the product below the first product (3 x 60 = 180). 
6. Next, multiply the tens digit of the multiplier by the ones digit of the multiplicand and write the product below the two products (20 x 5 = 100).
7. Lastly, multiply the tens digit of the multiplier by the tens digit of the multiplicand and write it under the previous three products (20 x 60 = 1,200). 
8. Add up the four partial products to obtain the final answer (15 + 180 + 100 + 1,200 = 1,495).

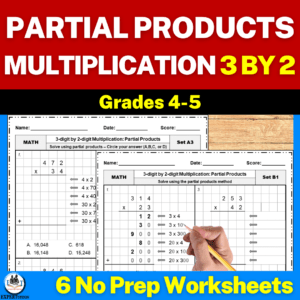
Partial Products Multiplication Practice Worksheets

If you’re looking for engaging partial products multiplication worksheets to use with your students, then my differentiated practice worksheets will be the perfect fit for you.

You can get these multiplication products from my TPT store or my WooCommerce shop.

Area Model Multiplication Strategy

What is an area model?

An area model is a type of rectangular diagram or model used in mathematics to solve problems involving multiplication and division.

The factors or the quotient and divisor define the length and width of the rectangle. The area model is also known as the box model.

If a rectangle has a length of 25 units and a width of 18 units, then this area can be calculated by finding the product 25 x 18.

For simpler calculations, we can further divide this rectangle into smaller rectangles, and then add the areas of those smaller rectangles to determine the total area of the rectangle.

We can do this by breaking the lengths of the sides into smaller numbers using expanded forms.

Area Model Multiplication Examples

The following examples will help understand the concept of area model multiplication. 

Area Model Multiplication with a one-digit multiplier (54 x 2):

To multiply a 2-digit number by a 1-digit number using the area model, follow the given steps: 

1. Write the numbers in expanded form as tens and ones. (54 = 50 + 4), (2 = 2)
2. Draw a rectangle or a box with 2 columns.
3. Write the terms of the 2-digit number on the top of the rectangle, one on the top of each cell.
4. On the left of the rectangle, write the term of the 1-digit number on the side of the cell. 
5. Write the product of the tens and ones in the first cell (2 x 50 = 100).
6. Then, write the product of the ones in the second cell (2 x 4 = 8).  
7. Finally, add all the partial products to get the final product (100 + 8 = 108).

Area Model Multiplication with a two-digit multiplier (65 x 23):

To multiply two 2-digit numbers using the area model, follow the given steps: 

1. Write the numbers in expanded form as tens and ones. (65 = 60 + 5), (23 = 20 + 3)
2. Draw a rectangle or a box with 2 rows and 2 columns.
3. Write the terms of one of the numbers on the top of the rectangle, one on the top of each cell.
4. On the left of the rectangle, write the terms of the other number, one on the side of each cell. 
5. Write the product of the tens in the first cell. Then write the product of the tens and ones in the second and third cells. Write the product of the ones in the fourth cell.  
6. Finally, add all the partial products to get the final product.

Area Model Multiplication Practice Worksheets

If you’re looking for engaging area model multiplication worksheets to use with your students, then my differentiated practice worksheets will be the perfect fit for you.

You can get these multiplication products from my TPT store or my WooCommerce shop.

The Long Multiplication Strategy

The long multiplication is also known as the standard or traditional algorithm.

This is the method usually accepted as the best method.

This method however, is prone to mistakes when students do not fully understand the steps.

Long Multiplication Examples

The following examples will help understand the concept of long multiplication. 

Long multiplication with a one-digit multiplier (54 x 2):

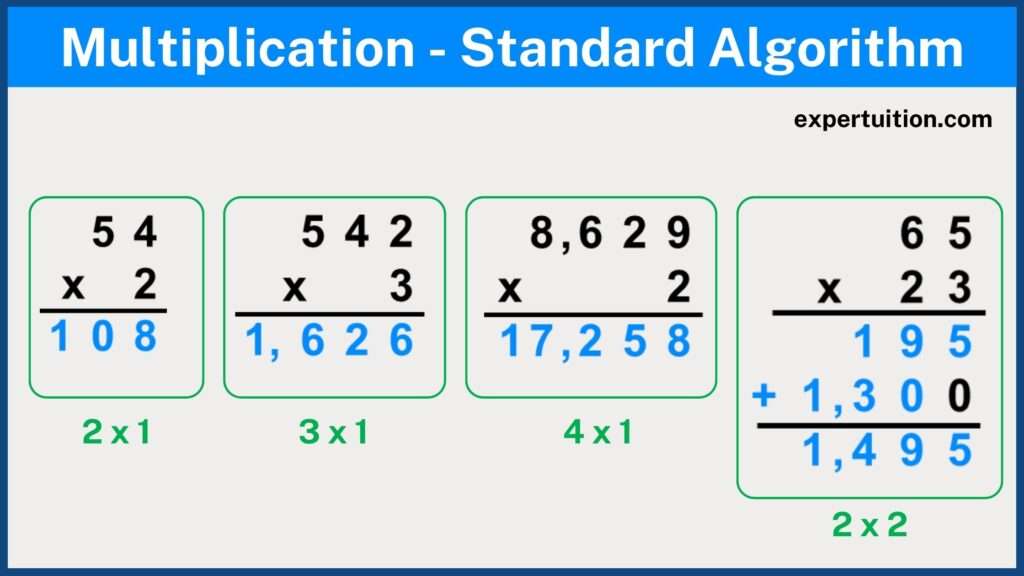
To multiply a 2-digit number by a 1-digit number using long multiplication, follow the given steps: 

1. Write the numbers vertically, one above the other. Make sure the place values are lined up. The number with the most digits should go on top.
2. Draw a horizontal line under the equation.
3. Multiply the digit in the ones place of the bottom number by the digit in the ones place of the top number (2 x 8 = 8). The product goes in the ones place below the line.
4. Multiply the digit in the ones place of the bottom number by the digit in the tens place of the top number (2 x 5 = 10). Since 10 is a two-digit number, the 1 must be ‘carried’ to the hundreds place.
5. There is no digit in the hundreds place of the top number to multiply by the digit in the ones place of the bottom number. Therefore, the 1 ‘carried’ to the hundreds place is written in the hundreds place of the product.
6. Now the top number has been multiplied completely by the bottom number (54 x 2 = 108).

If there are more than two digits in the top number, multiply the digit in the ones place of the bottom number by the remaining digits in the top number in order (hundred, thousands, ten thousands, etc.).

If a product has two digits, the first digit should be ‘carried’ to the top of the next place.

Long multiplication with a two-digit multiplier (65 x 23):

To multiply two 2-digit numbers using long multiplication, follow the given steps: 

1. Write the numbers vertically, one above the other. Make sure the place values are lined up.
2. Draw a horizontal line under the equation.
3. Multiply the digit in the ones place of the bottom number by the digit in the ones place of the top number (3 x 5 = 15). The product goes in the ones place below the line. Since 15 is a two-digit number, the 1 must be ‘carried’ to the tens place.
4. Multiply the digit in the ones place of the bottom number by the digit in the tens place of the top number (3 x 6 = 18). Since 1 was ‘carried’ to the tens place, this must be added to get 19. Also, since 19 is a two-digit number, the 1 must be ‘carried’ to the hundreds place.
5. There is no digit in the hundreds place of the top number to multiply by the digit in the ones place of the bottom number. Therefore, the 1 ‘carried’ to the hundreds place is written in the hundreds place of the product.
6. Now the top number has been multiplied completely by the bottom number (65 x 3 = 195).
7. Repeat the steps using the digit in the tens place of the bottom number. The only difference is that since we are working in the tens place now, the product will begin in the tens place. Usually, a 0 is written as a placeholder in the ones place of the second product.
8. Write the product of 65 x 20 (1,300) under the first product.
9. Add the two products to get the answer (195 + 1,300 = 1,495).

Long Multiplication Worksheets (Standard Algorithm)

If you’re looking for engaging long multiplication worksheets to use with your students, then my differentiated practice worksheets will be the perfect fit for you.

You can get these multiplication products from my TPT store or my WooCommerce shop.

Some Common Errors of the Long Multiplication Strategy

One of the most common errors that students face is forgetting to add any carried digits to the product.

Another common error is that students start recording the second product in the ones place when the multiplier has more than one digit.

Conclusion

The ability to multiply is a life skill that kids need to develop at a young age in order to address difficulties in the real world, much like other mathematical operations. 

This post discusses three different multiplication strategies that can be used to multiply large multi-digit numbers.

Please leave this field empty

DOWNLOAD FREEBIES

Please, enter your NON-WORK EMAIL to ensure that you get the freebies!

First name *

Email Address *

We don’t spam! Read our privacy policy for more info.

Check your inbox or spam folder to confirm your subscription for the link to freebie library.